알고리즘 소개

컴퓨터과학에서 알고리즘이란

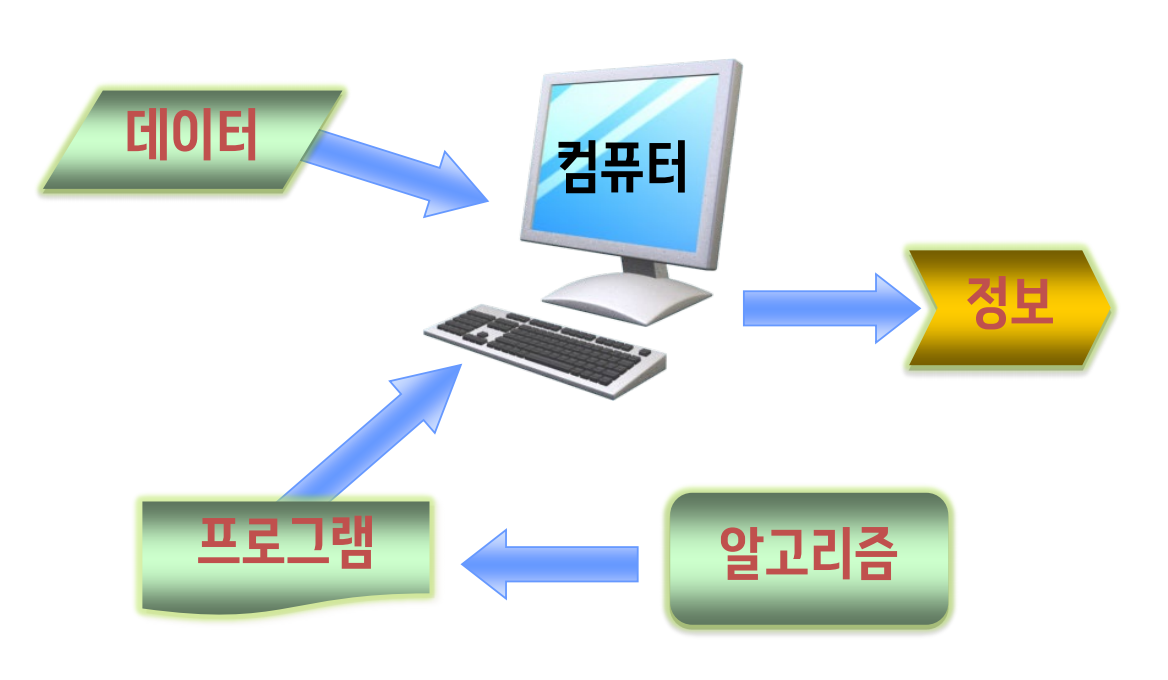
• 컴퓨터과학 = 컴퓨터 + 데이터 + 프로그램 + 알고리즘
• 컴퓨터의 한계 ≒ 알고리즘의 존재 여부
• 컴퓨터 과학 = 알고리즘 과학

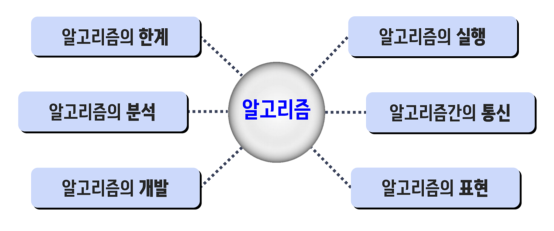
기본 개념

서울에서 부산에 가려고 한다. 그러면 어떻게 갈건지에 대한 일련의 과정을 거쳐야 한다. 버스, 기차, 자차 등 교통 수단을 선택하고, 고속도로, 국도 중 어떻게 갈건지 등 많은 것을 선택하고 순서를 정해야 한다. 이처럼 아무리 간단한 문제일지라도 문제를 해결하기 위해서는 "일련의 단계적인 처리 과정"이 요구된다.

 

한편, 같은 문제가 발생해도, 부여되는 조건에 따라 처리 과정은 달라질 수 있다. 앞선 예에서, 짐이 많다던지, 누구와 동행해야 한다던지, 몇시까지 도착해야 하는 등 상황에 따라 방법이 달라질 수 밖에 없다. 

 

알고리즘은 음식을 만드는 조리법에 많이 비유된다. 식재료(데이터)가 준비되면 조리법(알고리즘)을 따르면 음식이 만들어지듯 문제을 해결한 결과를 얻기 때문이다.

• 잘 알려진 "특정 문제"를 위한 알고리즘의 설계 및 분석 방법 이해
• 컴퓨터를 이용한 문제 해결 방법에 대해 체계적으로 생각하는 방법 이해
• 주어진 문제에 대한 지적 추상화 능력 및 통찰력 향상

컴퓨터과학이란

• 컴퓨터를 활용해서 주어진 문제를 해결하기 위한 학문

알고리즘이란

• 단계적인 처리 절차를 따르면 주어진 답을 구할 수 있다.

문제 사례

• 최솟값(최댓값) 찾는 문제
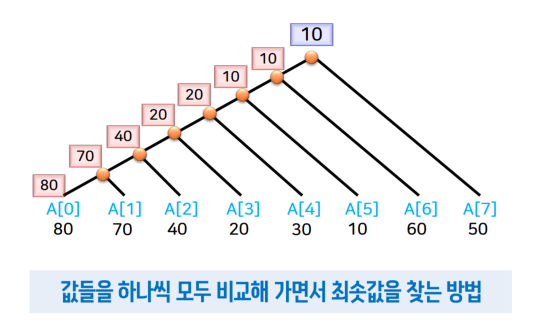
  A[  ] = {80, 70, 40, 20, 30, 10, 60, 50}
  1. 입력 배열 중에서 첫 번째 데이터를 최솟값(최댓값)으로 지정
  2. 배열에서 다음 숫자를 읽고, 이것과 저장된 초솟값(최댓값) 비교
  3. 비교 후 더 작은(큰) 숫자를 최솟값(최댓값)으로 다시 지정
  4. 배열에 처리할 데이터가 남아 있으면 2번째로 다시 시작
  5. 저장된 최솟값(최댓값)을 결과로 출력
• 한 점 그리기 문제(오일러 경로를 문제, 퀘닉스버그 다리 문제로 불림)
  그래프의 모든 간선을 오직 한 번씩만 지나가는 경로(점의 방문은 여러 번 허용)
  

  

  

  • 오일러 경로의 존재 여부를 확인 규칙
    • 각 정점의 차수(해당 정점에 부수된 간선의 개수)가 홀수인 정점이 0 이거나 2개이면 오일러 경로 존재
    • 만약 홀수인 정점이 2개일 경우 반드시 홀수 정점에서 시작
    • 특히 홀수 정점이 0개인 경우에는 출발점과 도착점이 같은 오일러 경로가 된다(오일러 회로)
    • 홀수 정점이 2개 초과이면 오일러 경로가 존재하지 않는다.
• 최단 경로를 찾는 문제
  
  

  

  
  
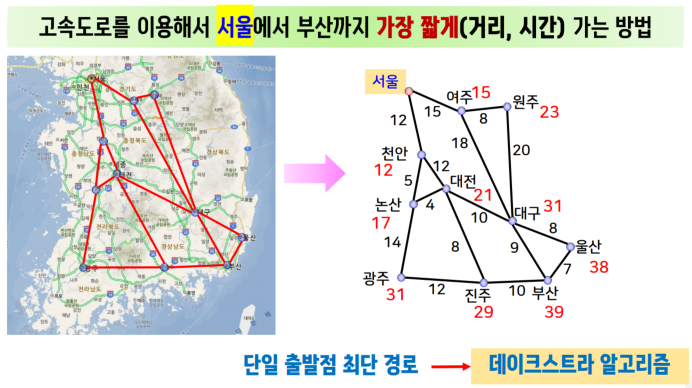
  • 하나의 출발점을 기준으로 다른 모든 정점(도시)으로의 최단 경로를 구하는 문제는 데이크스트라(다익스크라) 알고리즘으로 해결할 수 있다.
    • 서울 - 천안- 논산 - 대전 - 진주 - 부산이 최단 경로이다.
  • 모든 정점 쌍 간의 최단 경로, 즉 임의의 최단 경로를 찾는 문제는 플로이드 알고리즘을 적용한다.

문제 풀이 과정인 알고리즘을적절한 프로그래밍 언어로 표현해서 컴퓨터가 이해하고 실행할 수 있도록 만든 "명령어의 모임"이 바로 프로그램이다. 

알고리즘이란 문제 해결을 위해 따라야 할 명령어들을 단계적으로 나열한 것

알고리즘의 조건

• 입출력 : 외부에서 0개 이상의 입력을 받아서 하나 이상의 출력을 생성해야 한다.
• 명확성 : 각 명령은 모호하지 않고 단순 명확해야 한다.
• 유한성 : 한정된 수의 단계를 거친 후에는 반드시 끝나야 한다.
• 유효성 : 모든 명령은 컴퓨터에서 수행할 수 있어야 한다.

알고리즘은 주어진 문제에 대한 하나 이상의 결과를 생성하기 위해 모호하지 않고 단순 명확하며 컴퓨터가 수행할 수 있는 유한개의 일련의 명령어들을 순서에 따라 구성한 것이라고 정의할 수 있다. 

an orderd set of unambiguous, executable steps that produce a result and terminates in afinite time

 

알고리즘이 존재한다는 것은 적어도 이론적으로는 주어진 문제의 해를 구할 수 있다는 관점에서 중요하다. 그리고 효율적이어야 한다. 현실적인 시간 내에 원하는 결과를 얻기 위해서는 효율적이어야 한다.

알고리즘 설계

• 입출력 조건과 처리 조건 등을 고려해서 문제 분석
• 알고리즘 설계 - 상향식 설계, 하향식 설계, 욕심쟁이 방법, 분할정복 방법, 동적 프로그래밍 방법 등...
• 정확성 검증 - 수학적 증명
• 효율성 분석 - 공간 복잡도, 시간 복잡

 

최솟값을 찾는 위의 두 가지 방식은 비교 횟수가 똑같다.  n개의 숫자 중에서 최솟값(최댓값)을 찾기 위해서는 최소 (n-1)번의 비교가 필요하다.

조건에 따라 달라지는 알고리즘

뒤섞인 카드에서 원하는 숫자를 가진 카드를 찾는 경우

무작위 배치	정렬  배치
SequentialSearch (A[ ], n, key) 입력 A[0..n-1] : 입력 배열 n : 배열 크기(데이터 개수) key : 탐색 키(찾으려는 값) 출력 key가 배열 내에 존재하면 해당 인덱스, 아니면 n을 반환 {   i = 0;   while ( i < n && A[i] != key)      i = i + 1;   return (i); }	BinarySearch (A[ ], key, left, right) 입력 A[left..right] : 입력 배열 key : 탐색 키 출력 key가 A[ ] 내에 존재하면 해당 인덱스, 아니면 -1을 반환 {   if( left > right) return (-1);   Mid = [ (left_right) / 2]; // [x]는 소수점 버림(floor 연산)   if (A[Mid] == key) return (Mid);   else if (key <  A[Mid]) BinarySearch(A, key, left, Mid-1)           else BinarySearch(A, key, Mid+1, right); }
순차 탐색	이진탐색

• 순차 탐색
  • 처음 부터 순차적으로 확인
  • 운이 좋으면 처음에 발견하겠지만 최악의 경우 마지막까지 확인해야 한다.
• 이진탐색
  
  1. 주어진 배열에서 중앙 위치를 계산
  2. 중앙 위치의 값과 탐색 키를 비교하고 원하는 값이라면 탐색 종료
  3. 중앙 위치의 값이 찾는 값이 아니면 탐색 키와 중앙의 값의 크기를 비교하여 이진 탐색을 순환 호출
  4. 탐색 키가 중앙의 값보다 작다면 탐색 키는 정렬된 입력 배열의 왼쪽 절반 부분에 존재할 수 있으므로 배열의 왼쪽 절반 부분 A[ left .. (Mid-1)]을 다시 입력 배열로 사용해서 이진 탐색을 수행
  5. 탐색 키가 중앙의 값보다 크다면 배열의 오른쪽 절반인 A[ (Mid+1)..right]를 대상으로 이진 탐색을 순환 호출

알고리즘의 설계는 주어지는 문제와 조건 등에 따라 매우 다양해질 수 있으므로 모든 문제 혹은 대부분 문제에 대해서 일반적으로 적용할 수 있는 범용적인 개념의 알고리즘 설계기법은 불행하게도 존재하지 않는다.

대표적 설계기법

• 욕심쟁이 바업
• 분할정봅 방법
• 동적 프로그래밍 방법